Nel nostro excursus circa la ricorrente applicazione della sezione aurea nella scultura intendiamo mettere in rilievo lo stretto legame che vi è tra il lavoro del matematico e quello dell'artista. Il matematico, come il poeta o il pittore, crea inseguendo un suo ideale estetico. La matematica viene quindi presentata attraverso uno dei suoi aspetti meno noti, quello della bellezza, del suo connubio con l'arte e la scultura in particolare.Pitagora diceva: "se il numero è ordine, come accordo di elementi illimitati e illimitanti, e se tutto è determinato dal numero, tutto è ordine".

• Tuttavia sarebbe riduttivo pensare che solo i Greci applicassero consapevolmente i rapporti del rettangolo aureo nelle loro opere scultoree; infatti gli Egiziani furono i primi fruitori di questo canone geometrico, destinato a costituire un Leitmotiv nella concezione dell'arte nell'Occidente (anche se non è improbabile che presso altre culture si sia applicata la proporzione del rettangolo aureo).

In questo percorso prenderemo in esame alcuni capolavori scultorei prodotti da due civiltà mediterranee che nella loro vastissima produzione artistica si sono servite di questo canone: gli Egizi e i Greci.

GLI EGIZIANI
LA STELE DEL RE GET

Ars sine Scientia nihil est: l’arte senza la Scienza è nulla. La celebre frase fu pronunciata nel 1399 dal Maestro Giovanni Mignot, architetto parigino, chiamato a Milano per valutare l’opera della fabbrica del Duomo. Si accese una disputa con le maestranze locali sulle proporzioni da dare ai contrafforti in rapporto al tipo di pietra usata, e nel corso della disputa il Maestro Mignot pronunciò questa celebre frase, in cui «arte» significa tecnica e «scienza» indica la geometria.

Mignot non intendeva certo affermare nulla di nuovo, si limitava a ribadire una sapienza custodita da secoli che già eccheggiava nell’unico frammento dello scultore Policleto che la storia ci ha restituito: «l’arte si ottiene con molti numeri e badando ai minimi dettagli».

L’unico modo per documentare l’uso di teorie geometriche nell’arte è quello di impugnare squadra e compasso per individuare se l’opera è frutto di un sistema coerente. Circa la stele del re Get osserviamo che la sua limpida scansione sembra scaturire dalla sezione aurea, che si intravede soprattutto nel rettangolo che circoscrive il palazzo e il glifo del re: il serpente.Nella stele, proveniente da Abido e oggi al Louvre, è iscritto il nome del re Get, della prima dinastia e indicato col serpente, sul quale è il falco del dio Horus.In età antica, almeno nel mondo greco, la simmetria indica solamente, che l’opera è costruita con lo «stesso metro», ovvero con lo stesso modulo. Una semplice proporzione armonica come 1:2, ‘asimmetrica’ per il mondo moderno, è invece perfettamente ‘simmetrica’ nel mondo antico: perché è commensurabile con lo stesso modulo.
Una concezione dinamica della simmetria, dunque, di cui la stele del re Get è squisita e sapiente testimonianza: si osservi nell’immagine sottostante come la mediana della stele scandisca il ritmo delle colonne secondo un ritmo armonico d’ottava, o 1:2.
In realtà il modulo che informa la stele non è aureo, ma deriva da un processo chiamato dinamizzazione del quadrato: proiettando la sua diagonale si ottiene un rettangolo il cui lato maggiore è pari alla diagonale del quadrato originario. Questo processo, che può essere ripetuto ottenendo  rettangoli in radice di 2, 3, 4, è tipico degli avori tardo romani, dei fregi bizantini e delle composizioni medievali. La stele di Get ci offre dunque un precedente storico di rilevante interesse. Si tratta di una composizione i cui rapporti vengono tutti stabiliti mediante archi di cerchio e proiezioni dei loro raggi. Tuttavia anche la proporzione aurea vi svolge un ruolo non secondario: sia nell’assetto di Horus che nel rettangolo del Palazzo; il rettangolo in cui ondeggia il serpente è in rapporto aureo col quadrato costituito dal palazzo: il re è la parte ‘aurea’ della terra regale; agli Egizi non sfuggivano le proprietà correlate alla Sezione Aurea: fattore costante e armonico di crescita. Ciò significa dunque che l’arte egizia già padroneggia con eleganza sistemi compositivi piuttosto articolati, capaci di armonizzare le proporzioni dinamiche con le auree e con le armoniche. Cosa tutt’altro che semplice se si considera che le proporzioni auree e dinamiche sono irrazionali, governate cioè da numeri infinitesimali, mentre le armoniche sono razionali, basate invece su numeri interi.

Tra gli aspetti peculiari della stele l’equilibrio dinamico, ottenuto attraverso il sapiente spostamento dell’asse della composizione; il rapporto tra micro e macrocosmo, tra cielo e terra, sottolineato dall’uso di rettangoli di medesime proporzioni per la stele e il palazzo del re; la sorprendente derivazione del rettangolo che circoscrive il Palazzo e il Re da due intersezioni apparentemente secondarie, che nondimeno dobbiamo considerare come «emanazioni» di Horus; infine l’uso della «tavola tripartita», ancor oggi gioiello del Maestro nella massoneria simbolica: segno inequivocabile che per millenni è stato uno dei segreti del mestiere. Quando ancora il mestiere era mysterium.

L’anonimo scultore egizio che scolpì la stele del Re Get è partito, come è frequente nei secoli successivi, da un quadrato. I modi di costruzione regolare del quadrato utilizzati sono in genere due: la sua inscrizione in un cerchio, o il suo sviluppo a partire da un lato. In questo caso è probabile che le dimensioni della stele abbiano indotto a costruirlo dal lato CD. Proiettati due archi di cerchio con raggio pari a CD, e due verticali da C e D, si determinano i punti A e B. Il formato della stele risulta da una dinamizzazione di questo quadrato originario ABCD: puntando il compasso in C e D con raggio CA e DB si determinano i punti F ed E di un rettangolo in radice di 2 (d’ora in poi V2): se assumiamo che il quadrato abbia misura 1, la sua diagonale, per il teorema di Pitagora, sarà pari a V2 . Poiché il rettangolo EFCD ha come lato minore quello del quadrato, e come maggiore la proiezione della diagonale, è detto rettangolo V2.
Dal rettangolo EFCD lo scultore ha proiettato le diagonali CE e DF, ottenendo l’intersezione G che fissa l’altezza della stele. È molto probabile che lo scultore si sia avvalso anche della sezione aurea. In questo caso, puntato il compasso sulle mediane M ed N del quadrato ABCD con raggio NA e MB, ha ottenuto i punti H e I. Si noterà che l’intersezione degli archi AI e BH, il punto L, è stato proiettato su IC ottenendo il punto S, che funge da base per l’arco di chiusura della stele. L’arco AI determina l’altezza di Horus, e la diagonale CA l’estremo per la coda. Sull’asse LS è impostato il suo vigile occhio. Le zampe si stringono tra la mediana GP e la sezione aurea QR. Per determinare questa misura lo scultore, dal rettangolo aureo HICD, puntato il compasso con raggio HA, ha ottenuto il punto Q e quindi il quadrato aureo HQRA (è «aureo» perché è in proporzioni auree con il quadrato maggiore ABCD).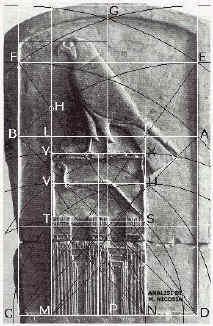

Sorprendente è il sistema d’individuazione del rettangolo, su cui poggia Horus, con il Palazzo Reale e il serpente. Dall’intersezione dell’arco BE con la diagonale DF del rettangolo V2, lo scultore ha tratto il punto H, e il punto I dalla intersezione dell’altra diagonale CE con il lato AB del quadrato di base. H e I, proiettati su CD, determinano i punti M ed N dai quali lo scultore ha ricavato il quadrato STMN. Questo quadrato è stato dinamizzato col medesimo sistema: puntando su M ed N con raggio MS ed NT, ha ottenuto il rettangolo V2 UVMN. Quindi con le diagonali MU ed NV ha determinato il rettangolo XYMN V3 che circoscrive Palazzo e Re. Sull’asse UV del rettangolo V2 è stato impostato il serpente. L’analogia non è casuale: sia il glifo del re Get, rappresentato dal serpente, sia Horus, suo omologo celeste, sono impostati sul rettangolo V2. La corrispondenza tra cielo e terra non potrebbe essere più netta.

Lo scultore utilizza anche la «tavola tripartita», ovvero il sistema di divisione tripartito dei lati d’un quadrato che genera una scacchiera di nove caselle. Il quadrato minore ABCD, diviso dalle due diagonali CA e DB, viene scandito dalle oblique che congiungono l’angolo con la mediana del lato opposto, come per esempio BE ed EC. L’intersezione di queste oblique con le due diagonali consente di individuare quattro punti che possono essere attraversati da due coppie di segmenti paralleli. In questo caso ci siamo limitati a segnare le due parallele verticali e l’orizzontale superiore. Su questa s’arrestano gli sgusci delle colonne, mentre le due verticali vengono usate per scandire il ritmo delle tre colonne. L’ampiezza della maggiore è pari al terzo centrale del quadrato ABCD.     

I GRECI
I Greci apprezzavano il rettangolo aureo per le sue proporzioni perfette e caratteri  magici  in quanto riproducibile geometricamente un' infinità di volte (illuminante esempio di questa proprietà del rapporto aureo è la stella a cinque punte che ebbe grande successo tra i Pitagorici). Questo principio matematico di bellezza, riflette appieno la genialità dello spirito greco che caratterizza gran parte delle opere scultoree del periodo classico.

FIDIA E IL PARTENONE

Fra gli artisti chiamati da Pericle ai lavori pubblici, Fidia,figlio di Carmide, scultore ingegnere architetto genio artistico fra i più completi è quello di maggiore prestigio. La sua gloria è affidata al Partenone, il tempio di Atena eretto con la sua collaborazione, da Ictino e Callicrate. L'edificio ancora conserva, nonostante le distruzioni e le spoliazioni, tutto il fascino che gli viene da una struttura equilibrata e proporzionata, in un miracoloso accordo di misure geometriche esatte e di un'ispirazione libera da regole fisse, viva, naturale. E' come se l'architettura si tramutasse in scultura per variare armoniosamente di effetti con il variare della luce. E ciò appunto è il messaggio e la conquista dello spirito Greco: armonia del vero e dell'ideale, di ciò che è momentaneo e di ciò che dura, del senso e dello spirito; le emozioni e i sentimenti vivono e mantengono il loro valore accanto al valore immortale della ragione e dell'idea. 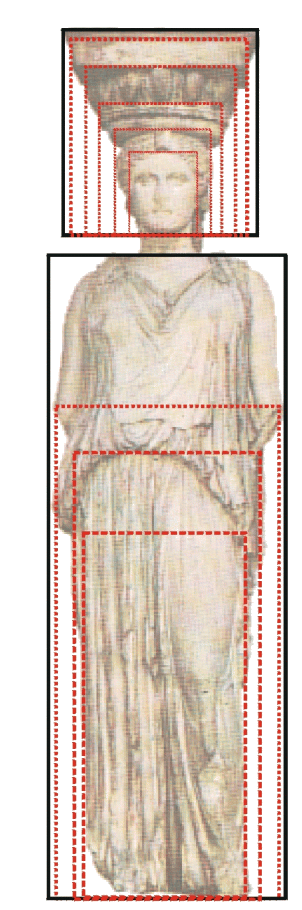Il Partenone il più celebre monumento dell'architettura Ellenica contiene molti rettangoli aurei e le stesse proporzioni auree si riscontrano nelle statue in esso presenti. Esempio significativo sono le Korai dell'Eritteo.

IL CANONE DI POLICLETO

Policleto, indicò come ideale supremo da perseguire la simmetria anatomica della figura umana, maschile e femminile, equilibrata nelle sue parti. Ignorando la lezione di Fidia e l'intensa carica emotiva espressa dalla sua opera,egli scrisse addirittura un canone in cui dava le misure perfette e assolute della figura umana: questa era concepita salda , atletica, armoniosa, con la testa piccola e la fronte larga, nella ricerca geometrica strutturale per la resa delle parti del corpo, vincolate tra loro da un rapporto dimensionale e di simmetria: la metà del corpo deve essere nell’attacco delle gambe, il piede è un settimo della lunghezza del corpo, la testa un’ ottavo, e la faccia un decimo. Il risultato, dice in un frammento rimasto di quest’ opera letteraria Policleto, dipende da una piccolezza decisiva in mezzo ai rapporti di proporzione.

La statuaria antica risente dell'influsso di questi grandi maestri, tenendo sempre maggiormente all'equilibrio perfetto e inalterabile di ogni composizione.