Il ragionamento compiuto da Pitagora si ricostruisce da Aristotele (Analityca priora 41a, 26-7) e da uno scolio al X libro di Euclide.

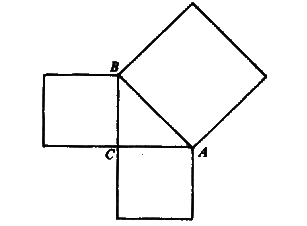
Dato un quadrato ABCD supponiamo, seguendo la teoria monadica, che la diagonale AC ed il lato AB siano commensurabili ne segue che la sottomultipla comune ai due segmenti AC e BC entrerà m volte in AC ed n volte in AB, dove m e n devono prendersi primi fra loro riducendoli ai minimi termini.

AC / AB = m / n

Ora, essendo AB = BC, per il teorema di Pitagora si ha che:

AC² = 2AB²

m² = 2n²

Si deduce che m² è pari, ma per la proprietà matematica per cui "il prodotto di due numeri dispari è dispari", anche m è pari. Se si ipotizza m uguale a 2p (dove p è un altro numero naturale) si avrà:

m² = 2n²

4p² = 2n²

2p²= n²

Risulta che n², e quindi n, è pari. Ma m ed n essendo primi tra loro non possono essere entrambi pari quindi l’ipotesi che AB e AC siano commensurabili, arriva ad una contraddizione, che seguendo il procedimento logico della dimostrazione per assurdo (reductio ad absurdum), nega la stessa tesi: in questo modo viene dimostrata l’esistenza di grandezze incommensurabili. Ma se m e n sono incommensurabili, cosa succede se si tenta di determinare il loro rapporto m/n? Riportando sulla diagonale prima n, poi 1/10 n, poi 1/100 n,... si ha: n<m; 1,4 n<m; 1,41 n <m; ... e così via all’infinito; cioè il rapporto tra grandezze incommensurabili è espresso mediante un numero decimale illimitato aperiodico (se fosse periodico sarebbe riducibile a frazione) che viene chiamato numero irrazionale.