



Questa prova compare nel IV libro della "Collezione Matematica" di Pappo di Alessandria (circa 300 a.C.)
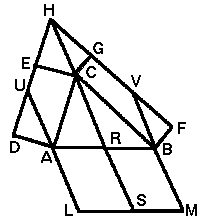 Ipotesi: ABC=triangolo
Ipotesi: ABC=triangolo
DE // AC e DE=AC
GF // CB e GF=CB
AL // HC e AL=HC
BM // HC e BM=HC
AD // EC e AD=EC
BF // CG e BF=CG
Tesi: ABML=CADE+CGFB
Non è richiesto che il triangolo ABC abbia un angolo retto e le figure costruite sopra i suoi tre lati sono arbitrariamente dei parallelogrammi invece di quadrati.
Si costruiscano i parallelogrammi CADE e CGFB rispettivamente sopra i lati AC e BC,
prolungando i lati AC e BC nel loro punto di incontro, dando origine ai segmenti EC e CG
congruenti fra loro e di lunghezza non precisata.
Si traccino poi i segmenti DA e FB dagli altri due vertici rispettivamente paralleli a CE
e CG e congruenti ad essi.
Si congiungano quindi i punti che andranno a formare i parallelogrammi.
Si prolunghino i segmenti DE e FG fino a farli incontrare in un punto H; quindi
congiungere il punto H con il vertice C e tracciare i segmenti UA e VB ad esso paralleli ,
a partire dai vertici A e B. Prolungando UA e VB si traccino i segmenti AL e BM paralleli
e congruenti ad HC, e RS parallelo e congruente a questi ultimi, ottenuto dal
prolungamento di HC.
Si costruisca infine il parallelogramma ABML congiungendo i punti L e M.
Considero CADE e CAUH:
AC in comune
l' altezza EC in comune
quindi CADE è equivalente a CAUH per il corollario
del teorema di equivalenza dei parallelogrammi.
Considero CGFB e CHVB:
CB in comune
l' altezza CG in comune
quindi CGFB è equivalente a CHVB per il corollario
del teorema di equivalenza dei parallelogrammi.
Considero CAUH e SLAR:
AL = HC per ipotesi
UC = AR perché comprese fra rette parallele
quindi CAUH = SLAR
Considero CHVB e SRBM:
HC = BM per ipotesi
CV = RB perché comprese fra rette parallele
quindi CHVB = SRBM
Ottengo che: CADE = SLAR e CGFB = SRBM per la proprietà transitiva e sempre per la
medesima proprietà, poiché SLAR + SRMB = ABML, ABML = CADE + CGFB.