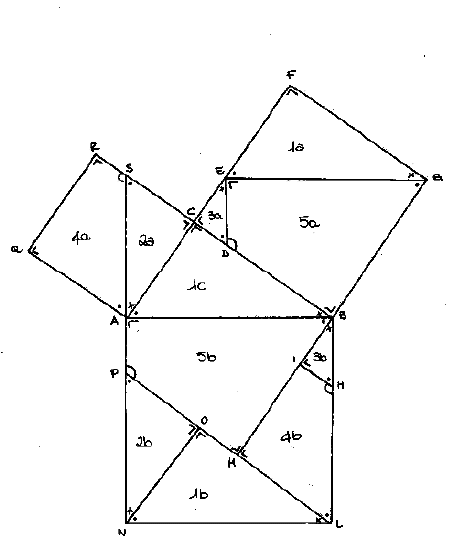
IPOTESI

ACB = 90°
QUADRATO COSTRUITO SUL CATETO MAGGIORE
GE // AB
DE perpendicolare EG
FEG = CAB perché entrambi corrispondenti
FGE = CBA perché entrambi corrispondenti
DEC = ABC perché entrambi complementari di FEG
EDC = CAB perchè entrambi complementari di DEC
EGB = CAB perché entrambi complementari di FGE
EDB = (ACB + ABC) perché entrambi supplementari di EDC

QUADRATO COSTRUITO SUL CATETO MINORE
SAC = CBA perché entrambi complementari di CAB
ASC = CAB perché entrambi complementari di SAC
QAS = CAB perché entrambi complementari di SAC
RSA = (ACB + ABC) perché entrambi supplementari di ASC.

QUADRATO COSTRUITO SULL' IPOTENUSA
PL // IH // CB
ON //BM //AC
BI = CE
CAB = ABM perché entrambi complementari di CBA
IBH = CBA perché entrambi complementari di ABM
BHI = CAB perché entrambi complementari di IBH
MLB  = CAB perché entrambi complementari di MBL
OLN  = CBA perché entrambi complementari di OLB
ONL  = CAB perché entrambi complementari di OLN
PNO  = CBA perché entrambi complementari di ONL
NPO = CAB perché entrambi complementari di PNO
APM  = ( ACB + ABC ) perché entrambi supplementari di NPO
INL  = ( ACB + ABC ) perché entrambi supplementari di IHB

TESI

1a+2a+3a+4a+5a = 1b+2b+3b+4b+5b

DIMOSTRAZIONE

1. Considero i triangoli 1a+1c
Essi hanno:
-CB=FG perché lati di uno stesso quadrato
-ACB=EFG perché entrambi congruenti a 90°
-ABC=EGF per ipotesi
Per il II° criterio di congruenza dei triangoli sono congruenti

Considero i triangoli 1b+1c
Essi hanno:
-AB=NL perché lati di uno stesso quadrato
-CAB=ONL per ipotesi
-CBA=OLN per ipotesi
Per il II° criterio di congruenza dei triangoli sono congruenti => per la proprietà transitiva 1a=1b.

2. Considero i triangoli 2a e 2b
Essi hanno:
-AC=ON per dimostrazione precedente
-NOP=ACS perché entrambi congruenti a 90°
-ONP=CAS per ipotesi
Per il II° criterio di congruenza dei triangoli essi sono congruenti

3. Considero i triangoli 5a e 5b
Essi hanno:
-CE=BI per ipotesi
-ECD=BHI perché entrambi congruenti a 90°
-IBH=CED perché entrambi congruenti a CBA
Per il II° criterio di congruenza dei triangoli essi sono congruenti

4. Considero i triangoli (MLB) e (ACB)
Essi hanno:
-AB=BL perché lati di uno stesso quadrato
-MLB=CAB per ipotesi
-MBL=CBA per ipotesi
Per il II° criterio di congruenza dei triangoli essi sono congruenti. In particolare  ML=AC e MB=CB

5. Considero i quadrilateri 4a e 4b
Essi hanno:
-ML=QA:ML=AC per dimostrazione precedente e QA=AC perché lati di uno stesso quadrato =>ML=QA per la proprietà transitiva.
-MI=QR:MB=CB per dimostrazione precedente e CB=CF perché lati di uno stesso quadrato =>  MB=CF per la proprietà transitiva. EF=AC per dimostrazione precedente e MI=EF per sottrazione di segmenti congruenti (CE e IB) => MI=AC per proprietà transitiva. Ma AC=QR perché lati di uno stesso quadrato => MI=QR per la proprietà transitiva.
-MLB=QAS perché entrambi congruenti a CAB
-LMI=AQR perché entrambi congruenti a 90°
-MIH=QRS perché entrambi congruenti a 90°
Per il criterio di congruenza dei poligoni essi sono congruenti

5. Considero i quadrilateri 3a e 3b
Essi hanno:
-AB=EG per dimostrazione precedente
-MB=BG:MB=CB per dimostrazione precedente e CB=BG perché lati di uno stesso quadrato => MB=BG per la proprietà transitiva
-ABM=EGB perché entrambi congruenti a CAB
-PAB=DEC perché entrambi congruenti a 90°
-PMB=DBG perché entrambi congruenti a 90°
Per il criterio di congruenza dei poligoni essi sono congruenti.