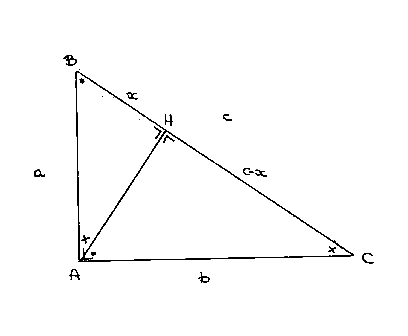
HP: BAC = BHA = AHC = 90°
ABC = ABH
ACB = ACH
TS: (AB)² + (AC)² = (BC)²

Considero i triangoli (ABH) e (ABC);
Essi hanno:
-BHA = BAC per ipotesi
-ABH = ABC per ipotesi

Avendo due angoli congruenti essi sono simili.

Considero i triangoli (ACH) e (ABC)
Essi hanno:
-CHA = BAC per ipotesi
-ACH = ACB per ipotesi

Avendo due angoli congruenti essi sono simili.

Per la proprietà transitiva sono tutti e tre simili tra loro. Ora si possono impostare le seguenti proporzioni
a : c = x : a   =>  x = a² /c
b : c = c- x : b  => c- x = b² /c 
x + (c- x) = c  => a² /c + b² /c = c  =>  a² + b² /c = c² /c   =>  a² + b² = c²

La similitudine ci permette di concludere la dimostrazione per via algebrica. Molte dimostrazioni del Teorema di Pitagora dicono che l’area del quadrato costruito sull’ipotenusa è uguale alla somma delle aree dei quadrati costruiti sui cateti. Non è necessario usare i quadrati per questa argomentazione. Basta sostituire i quadrati con altre figure simili le cui misure siano proporzionali ai tre lati del triangolo:
a² + b² = c² => sa² + sb² = sc²
[s corrisponde alla proporzione tra l’area di questa figura e quella del quadrato]