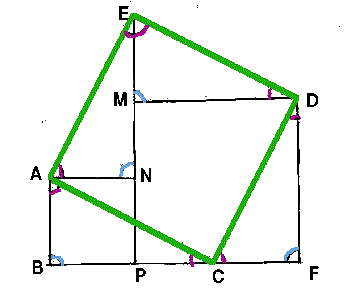
Ipotesi: ABC= triangolo rettangolo B=90°
Tesi: ABPN+PMDF=AEDC

Dimostrazione:
Considero il triangolo ABC
Costruisco il quadrato ACDE sull’ipotenusa ACÞ AC=CD=DE=EA.
Dal vertice D e dal vertice E traccio le perpendicolari DF e EP che si incontrano con BC.
Dal vertice D e dal vertice A traccio le perpendicolari DM e AN alla retta EP.
Si formano così quattro triangoli (ABC; CFD; DEM; ENA) congruenti.
Infatti poiché la somma degli angoli interni di un triangolo è 180° e ABC=90° (per ipotesi)Þ BAC+BCA=90°.

Considero il triangolo CDF
CFD=90° perché DF ^ BC Þ FDC+ DCF=90°; ma poiché DCF e ACB sono complementari dello stesso angolo ACD= 90° (perché angolo del quadrato ACDEÞ DCF+ ABC= 90°Þ BAC+ BCA=90° e BCA+ DCF= 90° Þ BAC =DCF) e poiché ABC+ BCA+CAB =180° e CFD+FDC+DCF=180° e CFD+FDC+DCF=180° e ABC=DCF=90° E BAC=DCFÞ CDF=ABCÞ poiché l’ipotenusa AC=CD (per costruzione)Þ per 2° criterio di congruenza dei triangoli ABC=CDF.

Considero i triangoli CDF e EDM
EDM=90° perché DM ^ EPÞ EMD=CFD
EDF=90° perché DF ^ MD ý Þ
EDC=90° perché angolo del quadrato ACDE
Þ EDM+MDC=90°
Þ MDC+CDF=90°Þ EDM=CDF.
Poiché la somma degli angoli interni di un triangolo è 180°Þ
Þ poiché EMD=90°Þ EDM+DEM=90° e poichèDCF+CDF=90° e CDF=EDMÞ
Þ MED=DCF e poiché CD=ED (perché lati del quadrato ACDE)Þ per 2° criterio di congruenza dei triangoli CFD=DEM.
Ma poiché ABC=DCF e DCF=EMDÞ per proprietà transitiva ABC=EMD.

Considero i triangoli EMD e AEN.
AED=90° perché angolo del quadrato AEDCÞ AEP+PED=90°
ANE=90° perché AN^ EP
Poiché la somma degli angoli interni di un triangoli 180°Þ
MED+EDM=90°
ý Þ per propietà transitiva AEM=EDM
AEN+NED=90°
E poiché AEN+EAN=90° e NED+EDM=90° e DEM+AEM=90°Þ
NED=EAN e poiché ED=EA perché lati del quadrato ACDE per 2° criterio di congruenza dei   triangoli ANE=MED.
Ma poiché ABC=MED e MED=ANE Þ per proprietà transitiva ANE=ABC

Considero AEN=ABC
ABC=90° (per costruzione)
ANE=90° perché AN+EP
CAE=90° perché angolo del quadrato ACDE Þ EAN+NAC=90°
Þ BAN=90° perché angolo del quadrato BPNAÞ BAC+NAC=90°
Þ ENA=BAC e poiché NEA+NAE=90° e BAC+BCA=90° e BAC=ENAÞ BCA=AEN
poiché AC=AE perché lati del quadrato ACDE per 2° criterio di congruenza dei triangoli ABC=ANE
e poiché ANE=EMD e ANE =ABCÞ per proprietà transitiva EMD=ABC
Quindi  i quattro triangoli (ABC, CDF, EDM, AEN) sono congruenti.
Allora ABPN e PFDN sono i quadrati costruiti sui cateti di ABC.
Il quadrato ACDE costruito sull’ ipotenusa AC è formato da ANE+MED+CANMD
Þ La somma di ABPN e PMDF è data da ABC+DCF+CANMD
Þ poiché i quattro triangoli sono congruenti e CANMD è comune Þ
Þ ABPN+PMDF=ACDE.