In ogni triangolo rettangolo il quadrato costruito sull'ipotenusa è equivalente alla somma dei quadrati costruiti sui cateti.
Ipotesi: r = AO
h = CH
CHO = 90°
Tesi: OC2 = CH2 + OH2
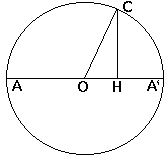
I tre punti A, C e A' situati sulla circonferenza formano a loro volta un triangolo rettangolo con CH altezza relativa all'ipotenusa e AA' = (AO + OH)+(A'O - OH).
Per il secondo teorema di Euclide:
CH2 = AH · HA'
AO=OA'=OC=>AH=OC+OH
HA'=OA'-OH=>CH2=(OC+OH)·(OC-OH)
=>CH2=OC2-OH2