In ogni triangolo rettangolo il quadrato costruito sull'ipotenusa è equivalente alla somma dei quadrati costruiti sui cateti.

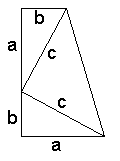
Ipotesi: AB=DE; AE=DC; CE=EB
EAB=CDE=90°
Tesi: calcolare l’area del trapezio.

Questa dimostrazione, scoperta da J.A. Garfield nel 1876, è una variazione della precedente. Si parte da un trapezio rettangolo avente come basi i due cateti e come altezza la somma di questi (ipotesi). Si deve calcolare l’area del trapezio tenendo presente che la formula è: "Somma delle basi per altezza diviso due".

(a+b)/2·(a+b)= ab/2+ab/2+c·c/2
semplificando si ha:
(a+b)²/2=2ab/2+c²/2
a²+2ab+b²–2ab=c²
quindi:
a²+b²=c²