I diagrammi dei numeri quadrati mostrano che, per costruire il II° quadrato (che rappresenta il numero 4) dal I° quadrato (il numero 1) si sono aggiunti 1 + 1 + 1 monadi. Aggiungendo 2 + 2 + 1 monadi al II° quadrato si ottiene il III° quadrato e così via. In generale per ottenere dal n-esimo numero quadrato l’(n + 1)-esimo numero quadrato bisogna aggiungere una riga di n monadi sotto, una colonna di n punti a destra e una singola monade nell’angolo (lo gnomone )

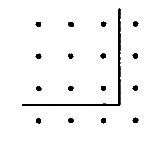
Così l’(n + 1) -esimo numero quadrato è più grande dell’ n-esimo di 2n + 1, ossia:

(n + 1)² = n² + (2n + 1)    *

Se 2n + 1 è un numero quadrato (2n + 1 = m²) compare una terna pitagorica:

(n + 1)² = n² + m²

n² + 2n + 1 = n² + m²

  n = (m² - 1) / 2

Da ciò deriva che

n + 1 = [(m² - 1) / 2] + 1

n + 1 = (m² - 1 + 2) / 2

n + 1 = (m² + 1) / 2

e da qui se, come detto sopra*, (n + 1)² = n² + (2n + 1),

[(m² + 1) / 2]² = [(m² - 1) / 2]² + m²

dove se ad m si assegnano numeri dispari si avranno terne pitagoriche, mentre i pari danno frazioni.