Questa è la seconda prova della lettera del Dr. Scott Brodie.

Prendiamo come conosciuto un teorema del "potere del punto": se un punto è preso fuori da un cerchio e si disegna dal punto un segmento tangente il cerchio e un altro segmento (ma secante) che taglia il cerchio in 2 punti diversi allora il quadrato della lunghezza della tangente è uguale al prodotto della distanza lungo la secante dal punto esterno al punto più vicino di intersezione col cerchio e la distanza lungo la secante al punto più lontano di intersezione col cerchio.

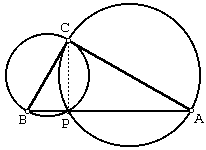Sia ABC un triangolo rettangolo con l’angolo retto in C: disegna l’altezza da C sull’ipotenusa; fai in modo che P indichi il piede di quest’altezza.

Poi dal momento che CPB è retto il punto P si trova sul cerchio con diametro BC; e dal momento che CPA è retto il punto P sta sul cerchio con diametro AC.

Perciò l’intersezione delle 2 circonferenze sui segmenti BC, CA del triangolo rettangolo originale coincide con P e in particolare sta su AB.

Chiama con x e y I pezzi dei segmenti BP e PA, rispettivamente, e come usuale, chiama "a", "b" e "c" le lunghezze dei lati di ABC rispettivamente opposti agli angoli A, B e C.

Perciò x+y=c.

Dal momento che C è retto BC è la tangente alla circonferenza con diametro CA e
il teorema del potere stabilisce che a²=xc; similarmente AC è tangente alla circonferenza con diametro BC e b²=yc.

Sommando troviamo a²+b²=xc+yc=c².