Questa è un’altra generalizzazione che non richiede angoli retti.

E' dovuta a Tabit ibn Qorra (896-902).

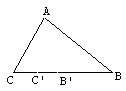Se gli angoli CAB, AC’B e AB’C sono uguali, allora AC²+AB²=BC(CB’+BC’). Infatti I triangoli ABC, AC’B e AB’C sono simili. Così abbiamo AB/BC’ = BC/AB e AC/CB’ = BC/AC che immediatamente riconduce all’identità richiesta.

Nel caso che l’angolo A sia retto il teorema si riduce al teorema di Pitagora e potrete rivedere direttamente la dimostrazione anche a questo indirizzo internet.