



Dimostrazione di B. F. Yanney (1903)
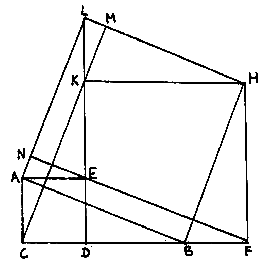 Dato il triangolo rettangolo (ABC) poggiante sul cateto maggiore CB, si
costruisca il quadrato dell’ipotenusa AB (ABHL), quindi il quadrato del cateto minore
AC (ACDE) dalla stessa banda di (ABC); si prolunghi BC di un segmento BF = CD e si
costruisca il quadrato di DF (DKHF), quindi si congiunga K con L, E con F e C con K.
Dato il triangolo rettangolo (ABC) poggiante sul cateto maggiore CB, si
costruisca il quadrato dell’ipotenusa AB (ABHL), quindi il quadrato del cateto minore
AC (ACDE) dalla stessa banda di (ABC); si prolunghi BC di un segmento BF = CD e si
costruisca il quadrato di DF (DKHF), quindi si congiunga K con L, E con F e C con K.
I triangoli (ABC) e (DEF) sono congruenti poiché hanno la stessa
base (per ipotesi CD = BF), la stessa altezza (AC = DE perché lati del medesimo quadrato)
e l’angolo tra essi compreso (= 90°). In particolare il triangolo (DEF) è translato
rispetto ad (ABC), quindi EF // AB. Il prolungamento della parallela di AB EF incontrerà
AL nel punto N. Analogamente si può dimostrare che anche i triangoli rettangoli (AEL) e
(CDK) sono congruenti e quindi
CK // AL. La parallela CK di AL incontrerà a sua volta LH nel punto M. I parallelogrammi
(LMOA) e (LKCA) hanno stessa base AL e stessa altezza LM, quindi Superficie di (LMOA) = Superficie di (LKCA); i parallelogrammi (LKCA) e (AEDC) hanno stessa base AC e stessa altezza
CD, quindi Superficie di (LKCA) = Superficie
di (AEDC).
I parallelogrammi ( HMOB) e
(HKCB) hanno stessa base BH e stessa altezza MH, quindi Superficie di (HMOB) = Superficie di (HKBC); i parallelogrammi (HKBC) e (HKDF) hanno stessa base KH e stessa altezza
KD, quindi Superficie di (HKDF) = Superficie
di (HKCB). Per la proprietà transitiva della
relazione di equivalenza, anche Superficie di (HMOB)
= Superficie di (HKDF).
Allora AC² + BC² = (LMOA) +
(HMOB) = (ABHL) = AB².

 Dato il triangolo rettangolo (ABC) poggiante sul cateto maggiore CB, si
costruisca il quadrato dell’ipotenusa AB (ABHL), quindi il quadrato del cateto minore
AC (ACDE) dalla stessa banda di (ABC); si prolunghi BC di un segmento BF = CD e si
costruisca il quadrato di DF (DKHF), quindi si congiunga K con L, E con F e C con K.
Dato il triangolo rettangolo (ABC) poggiante sul cateto maggiore CB, si
costruisca il quadrato dell’ipotenusa AB (ABHL), quindi il quadrato del cateto minore
AC (ACDE) dalla stessa banda di (ABC); si prolunghi BC di un segmento BF = CD e si
costruisca il quadrato di DF (DKHF), quindi si congiunga K con L, E con F e C con K.


